前回の記事に引き続き、今回も仮想通貨botの開発状況をまとめていきます。
今回はこちらの記事「仮想通貨botterのための必読書」に紹介されていた「アービトラージ入門」を再読してマインドマップを作ったので、改めて内容と感想をまとめました。

本書の中で私が重要だと感じた部分も整理しました。
学びの棚卸し。アービトラージの基本的な概念から、先物と絡めた実践的な分析までまとめられた良著でした。アビトラBotの開発に転用します。 https://t.co/MSw04Xql6c pic.twitter.com/o68CRAy6yg
— よだか(夜鷹/yodaka) (@yodakablog) February 3, 2024
1.基本概念
【裁定とは?】
・ある市場で資産を買い、他の市場で売る
・道理に合わない価格差から利益を得る
・ポジションやポートフォリオの新規構築および加工
・歪みを検知することが重要
・一物一価の法則(同じ投資商品なら価格も同じ)がベース
・一期待リターン一価の法則も歪みを見る上で重要
【ヘッジとは?】
・投資に伴うリスクを抑制、あるいは排除する行為
・利益をほぼ確定する戦略 ・ヘッジを行うことで損益に上限と下限を作る
【価格の歪みと収束】
収束の動きを駆動する過程には「構造的・絶対的な収束(真の裁定)」と「挙動・相関に基づく収束(リスクあり)」がある。
【裁定の実行】
単独の歪みと組み合わせ(ポートフォリオ)の歪みから最低機会を見つけることができる。単独の歪みとは、例えば地域によって金の価格が異なることなどを指す。これは運送費などの諸費用が原因で起こる。
組み合わせの歪みは一期待リターン一価の法則に基づいて分析される。裁定機械の条件は
①追加資金が不要
②ポジションが無リスク
③ゼロでない期待リターンがあること
ペアトレードでは時間経過による歪みの発生に注目することが重要。マルチファクターモデルが主流。
ポートフォリオ全体のリスク=個別資産のリスクの加重平均
【宿題1】
- 完全無リスクの裁定機会の発見には工夫が必要なのでそれをプログラムで解決する。
- 具体的にはマルチファクターモデルで市場を監視して裁定機会を検出するプログラムを書く。
- Github等で調べて先人が同じことをやっているかどうか確認する。
- 自力で2ファクターモデル監視のプロトタイプを作る。
2.キャリーコストによる価格評価
先物取引を絡めたキャリーコストモデルの利用を考える。
キャリーコスト:2種類の価格の間を取り持つコスト。スポット(現物)価格とフォワード(先渡し)価格・先物価格の間に生じる歪み。時間で差が出ることを利用する。費用(保険料・保管費用・資金調達コスト)や保有期間中の便益(配当・利息)が原因で生じる。
先物取引
先物取引(Futures Trading)は、金融市場で行われる派生的な取引の一形態で、指定された未来の日付に特定の資産(商品、金融商品、通貨など)を事前に定められた価格で売買する契約を結ぶことを指します。これにより、投資家は価格変動リスクから身を守ることができ、また価格の変動を利用して利益を得る機会を持つことができます。
先物取引の基本的な特徴
- 標準化された契約: 先物契約は取引所によって標準化されており、取引される資産の量と品質、契約の期間、満期日などの条件が定められています。
- マージン取引: 先物取引はマージンを用いて行われます。これは、取引全額を前払いするのではなく、契約価格の一部を担保金として預けることで契約を結ぶ方式です。これにより、少ない資金で大きなポジションを取ることが可能ですが、同時に高いリスクも伴います。
- 清算所による中央管理: 先物取引は取引所が中央管理し、取引所の清算所が各取引の当事者間でリスクを管理します。これにより、市場の透明性が保たれ、クレジットリスクが大幅に軽減されます。
- ヘッジングと投機: 先物市場は主に二つの目的で利用されます。ヘッジングは価格変動リスクから身を守るために使用され、投機は価格変動を利用して利益を得るために行われます。
先物取引の利用例
- 農業: 農産物の生産者や加工業者は、収穫物の価格が将来下がるリスクを避けるために先物市場で契約を結びます。
- エネルギー: 石油や天然ガスの生産者、消費者は価格の急激な変動に対処するために先物契約を使用します。
- 金融: 金利、株価指数、外国為替などの金融商品の価格変動リスクを管理するために先物契約が利用されます。
リスク
先物取引は高いレバレッジを活用するため、大きな利益をもたらす可能性がありますが、同時に大きな損失を招くリスクも非常に高いです。価格変動が予想と反対の方向に進むと、大きな損失を被ることがあります。そのため、先物取引は経験豊富な投資家や、リスク管理手法を理解している投資家に適しています。
先物取引は複雑でリスクが高いため、取引を開始する前にその仕組みやリスクを十分に理解し、適切なリスク管理戦略を用意することが重要です。
-

-
仮想通貨先物取引: 投資家にとってのチャンスとリスクを見極める方法
続きを見る
キャリーコストモデル
キャリーコストモデルは、特に先物市場において使用される価格決定モデルです。このモデルは、ある資産を現在から将来の特定の期日まで保有する際に発生する総コストを考慮して価格を算出します。このコストには、資産の保管、保険、財務コスト(金利)、およびその他の保有コストが含まれます。
キャリーコストモデルの基本
キャリーコストモデルでは、先物価格は基礎となる現物価格と保有コストを加えたもので決まるとされます。つまり、先物価格 F は以下のように表されます:
F=S+C
ここで、
- F は先物価格
- S は現物価格
- C はキャリーコスト(持続期間中の金利、保管費用、保険料等)
このモデルの背後にある考え方は、将来的に資産を購入する代わりに現在購入し、保有するために必要な追加コスト(キャリーコスト)を考慮に入れることです。
応用と意義
- 先物市場での価格決定: 先物契約の価格は、このモデルを通じて算出されることが多く、市場参加者が理論価格と市場価格の乖離を分析する際の基準として使用されます。
- 裁定取引: キャリーコストモデルを用いて、現物資産と先物契約の価格差を分析し、裁定取引の機会を探します。理論価格が市場価格よりも高いか低いかに基づいて、裁定戦略が立てられます。
- リスク管理: 企業が原材料や商品の価格変動リスクをヘッジするために、キャリーコストモデルに基づいた先物契約を利用することがあります。
限界と課題
キャリーコストモデルは基本的なモデルであり、すべての市場条件や変動を完全に説明できるわけではありません。市場の供給と需要の変動、予期せぬ経済イベント、政治的リスクなど、他の要因も先物価格に大きな影響を与える可能性があります。そのため、このモデルは他の分析手法と組み合わせて使用されることが一般的です。
キャリーコストモデルは、先物市場の理解に役立つツールの一つであり、資産の長期保有に伴うコストを考慮に入れた投資判断を可能にします。
【インプライドレポレートの利用】
「①スポットで買いフォワードで売る②1年間保有する③現物を引き渡してフォワード契約を決済する」場合の収益のこと。金利の期間構造にも応用可能。 この視点がキャリーコストモデルに基づいて裁定取引機会を見出す際に土台となる。
詳しい解説
インプライドレポレート(Implied Repo Rate)は、先物取引に関連する概念で、特に債券先物の市場において重要です。このレートは、現物資産(例えば国債)を現在の市場価格で購入し、それを保有しながら同時に先物契約を売る(ショートする)ことによって得られる理論上の利回りを示します。この取引は「キャッシュ・アンド・キャリー取引」とも呼ばれ、基本的には資産の購入と先物契約の売却から得られるリターンの差を表します。
インプライドレポレートの計算
インプライドレポレートは以下の式で計算されます:
Implied Repo Rate={(Cost of Carry+Income from selling futures−Cost of the cash bond) / Cost of the cash bond)}×(360 / days until futures settlement)
Implied Repo Rate = ((Futures Price - Cash Price) / Cash Price) * (360 / Days to Settlement)
ここで、
- Cost of Carry は保有コストを表し、金利コストや保管費用などが含まれます。
- Income from selling futures は先物契約を売ることから得られる収入です。
- Cost of the cash bond は現物債券の購入コストです。
- days until futures settlement は先物契約の決済日までの日数です。
用途と意義
- 裁定取引の機会の評価: インプライドレポレートを用いて、現物資産と先物契約の価格差を評価し、裁定取引の可能性を探ります。理論的なレポレートが市場のレポレートよりも高ければ、キャッシュ・アンド・キャリー取引による利益が期待できるため、投資家はこの機会を利用するかもしれません。
- 市場効率性の分析: インプライドレポレートは市場の効率性を評価する一つの指標としても機能します。理論価格と市場価格の乖離が大きい場合、市場に非効率性が存在することを示唆しています。
- リスク管理: 債券ポートフォリオを管理する際、インプライドレポレートは将来の価格変動リスクを評価するための重要なツールです。このレートを監視することで、ポートフォリオのリスクをより良く管理し、適切なヘッジ戦略を立てることが可能になります。
インプライドレポレートは、特に金融市場での先物取引において、価格の動きを理解し、投資戦略を練る上で重要な概念です。市場の小さな変動から大きな機会を見つけ出すために用いられるこのツールは、洞察力のあるトレーダーや分析家にとって非常に価値があります。
【キャッシュアンドキャリー裁定】
フォワード契約が割高な時に有効。
①資金をキャリーコストで借り入れて商品を現物市場で購入する
②フォワード契約の受け渡し日まで保有する
③フォワード契約に基づいて商品を売却し、売却代金で借入金を返済する
→「フォワード契約-売却代金」が利益となる。
【リバースキャッシュアンドキャリー裁定】
フォワード契約が割安な時に有効。
①フォワード契約を購入する
②現物市場で商品をショート(空売り)
③売却代金をキャリーコストで受け渡し日まで投資する
④フォワード契約に基づいて購入した商品をショートで手仕舞う
→売却代金を無リスク金利で運用。
【レポレートの不完備性】
①投資期間中、レポレートは固定されていないし、通常、無リスク金利よりも高い
②空売りで得た資金を全額投資できないこともある
③取引コストを考慮していない
④保管できないタイプの財もある これらの点を考慮して戦略を組み立てる必要がある。
→執行コストの考慮が必要。
詳しい解説
インプライドレポレートは有用なツールですが、いくつかの不完備性や限界も存在します。これらの限界を理解することは、金融市場での取引戦略を立てる際に重要です。以下に主な不完備性を挙げます。
1. 市場条件の変動に対する感応性
インプライドレポレートは静的な計算に基づいており、市場の状況が変化するとすぐにその変化を反映できない場合があります。市場のボラティリティが高まると、インプライドレポレートによる予測が実際の市場の動きと乖離する可能性があります。
2. モデルの仮定
インプライドレポレートの計算には多くの仮定が含まれています。これには金利の安定性、取引コストの無視、市場の流動性の高さなどが含まれます。これらの仮定が現実と一致しない場合、レポレートの計算結果が実際の市場の状況を正確に反映しないことがあります。
3. リスク要因の無視
インプライドレポレートは、市場のリスク要因や不確実性を完全には考慮していません。たとえば、政治的な変動や経済的な不安定性が予測に大きな影響を与える可能性がありますが、これらはレポレートの計算には直接組み込まれません。
4. 実際の取引コストとの差異
インプライドレポレートの計算では、しばしば取引コストが無視されます。しかし、実際の取引では手数料や税金、スプレッドなどが存在し、これらが取引の利益を減少させる要因となります。これらのコストが計算に含まれていない場合、実際の裁定取引の利益は理論値よりも低くなることがあります。
5. 法規制や取引制限の影響
市場には法規制や取引制限が存在することが多く、これらがインプライドレポレートに基づく取引戦略の実行を制限する場合があります。例えば、特定の資産に対するショートセリングの制限や、資本規制などが影響を与えることがあります。
インプライドレポレートは、特定の市場環境や条件下での取引戦略を計画する際の一つの指標としては有用ですが、その他の市場分析ツールやリスク管理戦略と組み合わせて使用することが重要です。これにより、市場の動きに対する理解を深め、より効果的な投資決定を行うことが可能になります。
【雑感1】
金利の歪みを早期に検知して高速で取引を繰り返すBotを作れば儲かる。執行コスト分析とリスク管理のロジックが重要。戦略執行コストを徹底的に洗い出して、それらを上回る収益を上げられるロジックを組むとよい。金利差が生じる要因を分析して裁定機会を早期に予測することがエッジになる。
フォワード契約が割高か割安かを判断する指標が不明瞭なので、この点は詳細な分析と根拠が必要。分析の視点やノウハウを勉強・蓄積するのは今後の課題。 金利面での理解が浅いので、先物契約の具体例をいくつか学んでイメージモデルを固める。
3.プット・コール・パリティ
ユーロピアン・オプションが土台。株式・プット・コール・財務省証券の要素からなる。オプションの権利行使期間とそれに等しい残存期間を持つ財務省証券の金利等を絡めて将来の関係性予測から資産価値を算出することで歪みを見出し裁定機会を発見することができる。
実際にはロング・ショートと組み合わせることで、本物のポジションを持たずにキャッシュフローを複製することが目的となる。プット・コール・パリティ関係式を変形することで、株式・プット・コール・財務省証券の4要素のうち3要素から残りの1要素を算出し、価値の歪みを見出す。
本物のポジションを擬似的に作り出した「合成資産」は規制裁定の機会を生む。例えば、融資の合成で本来規制されるような金利を生み出す手法を合法的に成立させられる可能性がある。「合成資産」の要素は「キャッシュフローの大きさ」と「裏付けとなるポジションの価値の変動に対するキャッシュフロー」。
「異なる要素の合成であっても権利行使日に同じペイオフが発生する」という視点から裁定機会を見出す。オプションの権利行使日における価値の関係を表す式がプット・コール・パリティ関係式。(具体的な式は本書を参照)合成ポートフォリをの代わりに連動ポートフォリオを組んだ方が安く済む場合がある。
確率を用いて導くのは、物事が発生する真の確率ではなく「上昇や下落の大きさ」である。
→コスト分析やリスク管理に応用できそう。
プット・コール・パリティは、金融のオプション理論における基本的な原則の一つで、ヨーロピアンスタイルのプットオプションとコールオプションの価格関係を説明します。この原理は、特定の条件下でオプションの価格がどのように関連しているかを示し、オプションの公正価格を理解するのに役立ちます。
プット・コール・パリティの公式
プット・コール・パリティの関係は以下の公式で表されます。
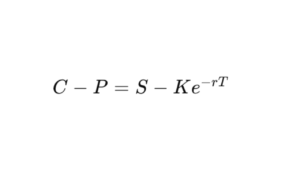
ここで、
- Cはコールオプションの価格
- P はプットオプションの価格
- S は基礎資産の現在価格(株価など)
- K はオプションの行使価格
- r は無リスク金利(年率)
- T は満期までの時間(年単位)
概念の理解
プット・コール・パリティは、オプションが満期になった際に、プットオプションとコールオプションの組み合わせが株を直接購入するのと同等の結果をもたらすという考えに基づいています。この関係を利用することで、市場におけるオプションの価格が過大または過小評価されているかどうかを判断することができます。
応用
プット・コール・パリティの原理は、オプション市場での裁定取引の機会を探す際に特に重要です。例えば、このパリティ関係が成立していない場合、市場に非効率性が存在することを示しており、裁定取引によってリスクなしに利益を得ることが可能です。裁定取引者は、過小評価されているオプションを買い、過大評価されているオプションを売ることで、価格の差から利益を得ることができます。
重要性
プット・コール・パリティは、オプションの価格が理論的にどのように決定されるべきかを理解する上で非常に重要です。また、この原則はオプション価格の安定性と市場の効率性を保証するのに役立ち、金融工学の領域で広く利用されています。
式の意味
式の意味の噛み砕いた説明
この式は、特定の時点でのコールオプションとプットオプションの価格差が、その資産を今買って将来売る(またはその逆)という戦略の利益またはコストに等しいことを示しています。簡単に言えば、コールオプションを買い、プットオプションを売ることのネットコスト(C−PC - PC−P)は、資産を現在の市場価格 SSS で購入し、無リスク金利 rrr で将来 TTT 年後の行使価格 KKK で売却(または逆に購入)する戦略の利益またはコストと等しいということです。
なぜ重要か?
このパリティ(均衡関係)を理解することで、オプション取引者は市場のオプション価格が理論的に正しいかどうかを判断することができます。例えば、この関係式に基づいて計算した結果と実際の市場価格が一致しない場合、オプションが過大評価または過小評価されている可能性があると判断でき、裁定取引の機会があるかもしれません。
実践的な応用
トレーダーはこの関係を利用して、オプションの価格が理論値から乖離している場合に裁定取引のチャンスを探します。例えば、コールオプションの価格が異常に高く、プットオプションの価格が低い場合、プットを買い、コールを売り、同時に基礎資産を買うことでリスクなしに利益を得ることができるかもしれません。
このように、プット・コール・パリティの式は、オプション取引において非常に実用的なツールとして機能し、市場の効率性や価格の公正性を評価するのに役立ちます。
戦略案
プット・コール・パリティの概念を仮想通貨のシステムトレードに応用する場合、その基本的な理論を活用して、オプションの裁定戦略やリスク管理戦略を展開することが考えられます。仮想通貨市場はそのボラティリティが高く、標準的な金融市場よりも価格の変動が激しいため、プット・コール・パリティを利用した戦略が特に有効に働く可能性があります。以下に具体的な戦略をいくつか挙げます。
1. オプション裁定戦略
プット・コール・パリティを用いて、仮想通貨オプション市場における価格の非効率性を見つけ出します。たとえば、プットオプションとコールオプションの価格がプット・コール・パリティの理論価格から逸脱している場合、以下のような裁定取引を考えることができます:
- パリティが示すよりもコールオプションが過大評価されている場合は、コールを売り、プットを買い、同時に基礎となる仮想通貨を買う。
- 逆に、パリティが示すよりもプットが過大評価されている場合は、プットを売り、コールを買い、基礎となる仮想通貨を売る(ショートする)。
2. ヘッジング戦略
プット・コール・パリティを利用して、仮想通貨ポートフォリオのリスクをヘッジします。例えば、仮想通貨の価格下落が予想される場合、プットオプションを購入して潜在的な損失を補償する一方で、コールオプションを売ってプレミアムを得ることができます。この戦略により、市場の下落リスクを効果的にカバーしつつ、オプションプレミアムによる収入も確保できます。
3. ボラティリティトレーディング
仮想通貨市場のボラティリティを利用して、プット・コール・パリティが示す理論値と実際の市場価格の差をトレーディングの機会とします。市場が極めてボラティルな時には、オプションの価格に大きな乖離が生じやすく、これを利用した短期トレードが可能です。
4. スプレッド取引
プット・コール・パリティを基にしたスプレッド戦略を用いて、オプション間の価格差を利用します。特定のプットとコールの組み合わせでスプレッドを構築し、市場の動きに対する露出を最小限に抑えつつ利益を狙います。
これらの戦略を実行するには、オプション市場の深い理解と、仮想通貨市場の動向に対する高い洞察力が必要です。また、仮想通貨市場の急激な価格変動によるリスクも考慮に入れる必要があります。システムトレードでは、これらの戦略を自動化し、市場の変動に迅速に対応することが可能です。
【宿題2】
- プット・コール・パリティ関係式を変形して裁定機会を算出するコードを書く。
- この関係式を作る発想を元にして、時間経過と金利の兼ね合いから価値の歪みを検出して戦略執行するBotのロジックを考える。
- 権利行使日における合成ポートフォリオの純価値を算出するコードを書く。
4.オプションの評価
オプションの評価方法は「2項モデル」と「BSM(プラックショールズモデル)」モデルの2種類がある。 どちらも配当を支払わない株式に対するユーロピアン・コール・オプション(満期日のみに権利行使できるオプション)でのキャッシュフローを合成する自己充足的で無リスクな裁定取引戦略に基づく。
両者が共通して扱う要素は
①株価
②オプションの権利行使価格
③将来の株価のボラティリティ
④無リスク金利
⑤権利行使期間
どちらのモデルも「オプションのペイオフを合成するポートフォリオを合成するのにかかるコスト」の形でコール・オプションの価格を評価している。
【2項モデルの基本】
原資産株式の価格変動とそれに応じたオプション・プレミアムの変動をオプションの権利行使期間中にわたってモデル化する。期初におけるオプション価格は期末における期待ペイオフの現在価値であると考える。 1期間モデルの理解が2期間〜他期間モデルへの理解につながる。
1期間での株価の変化率(上昇と下降)、期初の株価、期末の株価、期待ボラティリティ、金利、権利行使期間の長さに基づいて、ユーロピアン・コール・オプションの価値を算出する。 期末の株価は、平均ではキャリーコストに基づくフォワード価格を等しいと仮定する。(3章:「キャリーコストのよる価格評価」を参照)
適正なキャリーコストは与えられた期間に対応した無リスク金利であると仮定する。 上昇や下落の大きさを示すリスク中立確率を決める。 この場合の「リスク中立」は平均のペイオフを無リスク金利で割り引いてよいということ。投資家がリスク・プレミアムを求めないと仮定しているかのように考える。
ここで、株式のロングとコール・オプションのショートからなるポートフォリオを考える。 このポートフォリオは、株式のロングポジションによって市場の上昇に参加し、同時にショート・コール・オプションによって潜在的な損失を制限することを狙っている。
【株式のロング】
ロングとは、資産を購入することを指す。株式のロングポジションでは、投資家は株式を購入し保有することによって、株価の上昇を期待している。 株式のロングポジションは、株価が上昇すれば利益が発生し、逆に株価が下落すれば損失が発生する。
【コール・オプションのショート】
オプションは、将来のある時点で特定の価格で資産を買う(コールオプション)または売る(プットオプション)権利を与える契約。 コール・オプションのショートポジションでは、投資家は将来のある時点で資産を特定の価格で買う権利を他の投資家に売っている。
ショート・コール・ポジションは、株価が上昇しても損失が制限されるが、株価がある水準以上に上昇しないことを期待している戦略。逆に、株価が急激に上昇すると、損失が発生する。
【ヘッジレシオ:Hedge Ratio】
特定の投資ポートフォリオや取引戦略において、ヘッジとして使用される派生商品(通常はオプション)の数量を決定するための比率のこと。主にオプション取引において使用される。この比率は投資家がリスクをヘッジするためにどれだけのオプション契約を取るべきかを示す。
具体的には、ヘッジレシオは、保有している資産やポートフォリオの変動に対してどれだけのヘッジが必要かを示す指標。ヘッジは、通常、オプション契約を購入することによって行われる。このとき、ヘッジレシオは、オプションの契約数量を元のポートフォリオや資産の数量で割ったものとなる。
具体的な計算式は
ヘッジレシオ=数量(ヘッジに使うオプション)÷数量(元のポートフォリオや資産)
ヘッジレシオが1であれば、ポートフォリオ全体をヘッジするために必要なオプション契約の数量となる。ヘッジレシオが1より小さい場合、ヘッジのためのオプション契約はポートフォリオの一部をカバーする。
ヘッジレシオを適切に設定することで、投資家は市場の変動からくる損失を制限し、リスクを管理することができる。ただし、ヘッジが完全でないことやコストがかかることも考慮する必要がある。
株式のロングとコール・オプションのショートからなるポートフォリオでは無リスク金利に等しいリターンが実現する。ポートフォリオの価値は、株価が上昇しても下落しても、コールと株式の価値変動を差し引いたものになる。ここから導かれる数式でポーフォリオを無リスクにするヘッジレシオを算出できる。
すなわち、ヘッジレシオは
期末におけるコールオプションのばらつき÷期末におけるペイオフのばらつき
で求められる。ヘッジレシオは「コール・ショートの価値が変化するのを株式ロングの価値で相殺できる比率」であり、「無リスクのポートフォリオを作るための株式とコールの組み合わせ」でもある。
リターンが無リスク金利と等しくなければ、裁定取引機会が存在することになる。
(コールと原資産株式の組み合わせが無リスク金利になることを利用して、コール価格の評価を行う方法は後述) また、ヘッジレシオはコールオプションのデルタ(株価の変動に対するコールの感応度)も測っている。
【ヘッジレシオの分析】
ヘッジレシオという観点で分析することで
「ポートフォリオの変容」
「株価の動きへの反応」
「ポートフォリオ構築のコスト」
を明らかにすることができる。
【コールオプションのデルタ(Delta)】
オプション価格の変動に対する株価の変動の影響を示す指標。株価が1ドル上昇した場合、コールオプションの価格がどれだけ変動するかを表す。デルタは通常、0から1の範囲で表され、数値が大きいほど、オプション価格が株価の変動に敏感であることを示す。
デルタは「オプション価格の変動÷株価の変動」で計算される。例えば、デルタが0.5の場合、株価が1ドル上昇すると、コールオプションの価格は約0.5ドル上昇するという意味。デルタが0.8であれば、同じ株価の上昇に対してオプション価格が0.8ドル上昇することを示す。
デルタは単なる数値でなく、その符号も重要。コールオプションのデルタが正である場合、株価の上昇とオプション価格の上昇が正の相関関係にあることを示しているす。逆に、プットオプションのデルタが負である場合、株価の上昇とオプション価格の下落が負の相関関係にあることを示している。
【n期間の2項モデル】
2項モデルにおいては、期間の設定回数も重要。なぜなら、オプションの権利行使日におけるペイオフを計算し、そこから「後ろ向き」に時間を進んで帰納法で現在の価値を求めるから(「後ろ向き帰納法」)。
【権利行使期間における株価の上昇と下落】
リスク中立価格評価を行い、リスク中立確率を「期末の平均価格がキャリーコストに基づくフォワード価格に等しくなるよう」に求める。 この時、リスク中立確率に基づく将来の株価とキャリーコストに基づくフォワード価格が一致することを確認しておく。
【2項モデルは離散時間の設定に基づく】
2項モデルによるオプション評価は、時間を離散的なステップに区切り、各ステップごとに価格の変動をモデル化するアプローチを指します。これに対して、「連続時間モデル」では時間が無限に分割され、価格の変動が連続的にモデル化される。
2項モデルは、主にコックス・ロス・ルビンシュタイン(Cox, Ross, Rubinstein) モデルが知られている。これは離散的な時間ステップで価格の変動を捉える方法。このモデルは、時間をいくつかのステップに区切り、各ステップごとに資産価格が上昇または下落する確率を設定する。
例えば、期間がTでNのステップがある場合、各ステップごとに価格が上昇する確率(通常をp)、下落する確率(1-p)を設定する。このモデルでは、オプションの価格を逐次的に計算し、最終的な到達点から逆向きに計算していく。(「後ろ向き帰納法」)
離散的な時間ステップを使用することで、計算が比較的容易になり、オプションの価格を効果的に評価できるという利点がある。しかし、連続時間モデルに比べると厳密性が劣る場合がある。
一方で、連続時間モデルは計算が複雑であり、数値解析が必要。2項モデルはそのトレードオフとして、実用的な計算と一定の精度を提供する。
【BSMモデル】
連続時間の設定を使って、将来実現しうる株価を確率分布の形で表す。このモデルの強みは。オプションを評価する際に無限小の期間を使うことで、将来実現しうる株価の範囲を広げた点にある。
BSMモデルを実際に用いることを考えるのであれば、取引コストを考慮し、ヘッジ・ポジションの調整がもたらす費用と便益をバランスさせる必要がある。
【BSMモデルに必要な技術的な仮定】
- ユーロピアン・オプションにしか使えない
- 取引コストも税金も存在しない
- 無制限に空売りが可能である
- 株価は対数正規分布に従って確率分布する
- 株価は連続的に変化し、ジャンプすることはない
- 金利は一定である 株式は配当を支払わない
「株価は対数正規分布に従って確率分布する」とは、一般的には株価の対数変換が正規分布に従う傾向があるという意味。これはロバート・ブラウンの運動(ブラウン運動)に基づく仮定に基づいている。対数正規分布は、正規分布における対数変換が得られる確率分布のこと。

以下は、この仮定の背後にある概念の説明です。
1.ブラウン運動の仮定 ブラウン運動は、ランダムな変動が時間とともに独立に発生する現象をモデル化した数学的な概念。株価の変動もこのようなランダムな要素が組み合わさっていると仮定される。
2.対数正規分布への変換 対数正規分布は、正規分布の対数をとったものが正規分布に従う分布。対数を取ることで、株価の変動が対数スケールで一様であると仮定し、正規分布の性質を利用することができる。
3.対数変換の利点 対数変換によって、大きな価格変動と小さな価格変動の比率を均等に扱うことができる。これにより、過去の価格変動が将来においても同様に起こる可能性があるという考え方が反映される。
ただし、実際の市場では、対数正規分布が完全に成り立っているわけではない。実際の価格変動は、ブラック・ショールズ・モデルやその他のモデルによってより適切に記述されることがある。また、ブラウン運動の仮定は、市場の非効率性や価格変動のクラスタリングなどの現象を説明するのに十分ではない。
対数変換とは?
対数変換は、数学的な操作の一種で、ある数値や変数に対して対数(logarithm)をとることを指す。通常、自然対数(底がe)や10を底とする対数がよく使われる。株価の変動や金融データのモデリングにおいて、対数変換が使われる一つの具体例として、「収益率(またはリターン)のモデリング」がある。株価の変動を対数正規分布に近似するために、通常は「対数収益率」が用いられる。
【雑感2】
正しい評価方法を知ることで歪みを見出すことができる。オプションのように一見複雑なことであっても一つ一つの構成要素を丁寧に理解することで歪みを見出す手法が分かり、それが裁定機会を見つけることに繋がる。感覚にせよ理論にせよ、勝ち続けるためには勝ちに繋がる評価方法が必要。
初めて読んだときに「分からない」と思ったとしても、時間をおいて読み返すと大体分かるようになる。難しくて未経験の内容のものを読んで分からないと思うのは普通のことで、別の角度から学び直す機会を与えれば良いだけのこと。「この角度から学んでいては分からないかも」と切り替えることが大事。
「学び方を変えて別の方法でアプローチする」という手法は何かを上達させたいときに非常に有効である。例えば、「アビトラを実践してみる」とか「別の本でアビトラについて書かれたものを読んでみる」とか「アビトラについて書かれた論文を読んでみる」とか、できることはいくらでもある。
そうやって具体的なケースや解像度の高い捉え方をしている事例をたくさん蓄えることで、自分自身のアビトラに対する解像度を上げていく。知識を付けつつ実践経験を積むのが最も効率良く成長する方法。引き続き、実践経験の中で自ずと知識が付いていくスタイルにならざるを得ない環境設計をする。
【宿題3】
- 毎期そのときどきのヘッジ・レシオに合わせてポートフォリオを調整するコードを書く
- ポートフォリオの調整コストを算出するコードを書く
- 合成資産を戦略として採用する場合は、Botでポートフォリオの調整コストを下げる方法がないか検討する
6.裁定と資本構成の(無)価値
モジリアーニ・ミラー理論(MM理論)を土台にしてプット・コール・パリティを応用することで、裁定の(無)価値をプットやコールで表現することができる。
【ベースとなる考え方:その1】
企業が事業で得るキャッシュフローを受け取る権利を切り分けても、企業の価値は変わらない。企業の価値は実物資産で決まるのであり、実物資産を裏付けに発行する金融資産(証券)で決まるのではない。複雑な資本構成を構築するのにコストがかかる場合は、その構成に価値が付く。
レバレッジを使っても企業価値を高めることができるわけではない。レバレッジで期待リターンは上昇するが、同時に株主が負うリスクも上昇する。ここにはリスクとリターンのトレードオフが存在し、MM理論では数式によって表現されており、レバレッジをかける企業とかけない企業の価値は同じである。
【ベースとなる考え方:その2】
株主は企業資産に対するコール・オプションをロングしている。そして、債権者はそのコール・オプションをショートしていると捉える。 あるいは、株主はプットをロングし、債権者はそのプットをショートしていると捉える。
【企業の負債の価値】
これらの前提をもとに原資産が企業の資産であると定義すれば、株主の立場のコールとプットを用いた表現をプット・コール・パリティで結びつけて、「デフォルト・リスクを伴う企業の債権の価値=無リスク証券の価値−債権者が株主に対して売却したプットの価値」と定義できる。
【「デフォルト・リスクを伴う企業の債権の価値」とは?】
「デフォルト・リスクを伴う企業の債権の価値」とは、企業が債務不履行(デフォルト)する可能性があるというリスクを考慮した、その企業の発行する債券の現在価値を指す。
債券投資は、投資家が企業に資金を貸し付ける形で行われるが、企業が将来的に債務不履行に陥る可能性があるため、そのリスクを価格に反映させる必要がある。

以下にデフォルト・リスクを考慮した債券価値の要因を示します。
1.クレジット・スプレッド: デフォルト・リスクを反映した指標としてクレジット・スプレッドがある。クレジット・スプレッドは、無リスク資産(例: 政府債券)の金利と企業債の金利との差を示し、これが広がるほどデフォルト・リスクが高まっていると考えられる。
2.クレジット・レーティング: 企業の信用力を示すクレジット・レーティングは、債券のデフォルト・リスク評価に影響を与える。高い信用力を持つ企業は低い金利で債券を発行でき、逆に低い信用力を持つ企業は高い金利を支払わなければならない。
3.債券のデフォルト確率: デフォルト・リスクを詳細に見積もるためには、企業の将来的な債務不履行の確率を考慮する必要がある。これに基づいて、債券の現在価値が算出される。
4.デフォルト時の損失率: 企業がデフォルトした場合、債権者がどれだけの損失を被るかもデフォルト・リスクの一部。デフォルト時の損失率もデフォルト・リスクの評価に影響を与える。
【感想まとめ】
入門とありますが、私の経験不足で読み解くのが難しい部分もありました。 過去の経験と結びつけて『確かにそうだな』と思える内容も多かったです。しかし、血の通った学びにできる部分はまだまだ残っているのも事実。 実感を伴う知識に変えるために、あとは実践で確かめます。
良かった点は『この観点から分析するとこんなメリットやリスクがあるよ』という分析の構造がハッキリ書かれていることですね。これまで何となくの感覚でこなしていたことが理屈で説明できるようになる。説明のためのモデルを構築することの重要性が理解できます。理論を学ぶモチベも上がります。
分析モデルを闇雲に使うのではなく、「この環境ではこのモデルが有効ではないか?」という仮説を持って実践に臨めるようになる。 しかし、素人が小難しいことを考えていても行動が遅くなるだけなので、「現場で試す」→「理にかなっていたか?」という答え合わせ感覚で読み返します。一回で全てを理解しようとする必要はないのです。
本書はアービトラージという概念の解像度を高めるのに役立ちます。特に、先物市場における裁定機会の発見方法や合成資産の構築を絡めた複雑な概念を理解する手助けになります。 裁定の概念を理解することで「無裁定の状態」を説明できるようになります。
その説明を元に「本来あるべき状態」を逸脱した市場の歪みを認識できるようになり、それが「裁定機会」を見出すことにつながります。 プット・コール・パリティを用いた裁定戦略の拡張はBotにも応用可能だと思います。また、 現在の主要なDEXにも本書で扱う要素を含んだものがあるため、DeFiでも応用できそうです。
【宿題4】
- DeFiの主要なDEXで本書に出てきた要素を備えているものを探す
- MM理論の概要を勉強する
- 先物を絡めた市場で戦う場合は、単純な歪みを見出す前に「無裁定の状態」を定義するコードを書いてみる
