Bot トレードロジック 書籍・論文・web記事

仮想通貨botの開発記録#61(2024/3/3)「トレード戦略の基礎固め：経済数学の直観的方法(確率・統計編)まとめ」

2024年3月3日

前回の記事に引き続き、今回も仮想通貨botの開発状況をまとめていきます。

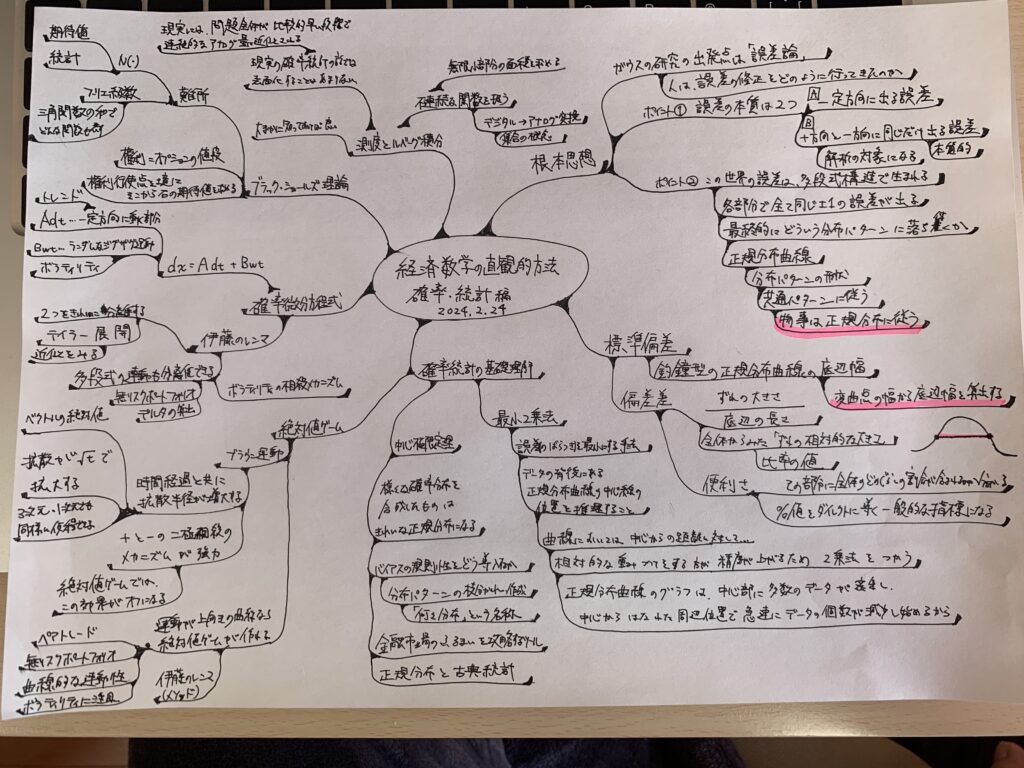
今回は「経済数学の直感的方法(確率・統計編)」を読んで、その内容をまとめました。

Yodaka

システムトレードをする際に重要になる観点が非常に多く学べる本でした。文系/理系それぞれの視点から説明されている内容でで、確率・統計を根本的な部分から深く理解することができました。

Yodaka

以前にまとめた「アービトラージ入門」とも関連性がある内容でした。

関連記事
仮想通貨botの開発記録#51(2024/2/3)「仮想通貨Botterの必読書シリーズ②アービトラージ入門」

続きを見る

【確率統計を理解するための根本思想】

  • ガウスの研究の出発点は「誤差論」
  • 「人は誤差の修正をどのように行なってきたのかを確かめる」というイメージをもつと分かりやすい
  • 誤差の本質は2つ。「一定方向に出る誤差」と「＋方向と−方向に同じだけ出る誤差」に大別できる。
  • 確率統計で解析の対象となるのは「＋方向と−方向に同じだけ出る誤差」
  • この世界の誤差は「多段式構造」で生まれる
  • 各部分で全て同じ±１の誤差が生まれる
  • 最終的にはどういう分布パターンに落ち着くかを見ることになる(正規分布曲線を用いる)
  • 世界のものごとのばらつきは正規分布に従う

【標準偏差】

標準偏差とは「釣鐘型の正規分布曲線の底辺幅」のこと。

変曲点の幅から底辺幅を算出することができる。

【偏差値】

偏差値とは、全体から見た「ずれの相対的な大きさ」のこと。

ずれの大きさ/底辺の長さ・比率の値とも言える。

【偏差値の便利さ】

偏差値の便利さは「その部分に全体のどのぐらいの割合が含まれるのかが分かる」ことにある。
→％値をダイレクトに導く指標になる

【確率統計の基礎理解】

1.最小２乗法

誤差を最小にする手法のこと。

  • データの背後にある正規分布曲線の中心線の位置を推理する。
  • 曲線においては、中心からの距離に対して相対的な重みづけをする方が精度が上がるため、２乗法を使う。
  • 正規分布曲線のグラフは、中心部に多数のデータが密集し、中心から離れた周辺位置で急速にデータの個数が減少し始める。
    →この前提に立つと、中心から離れたデータの重みづけをするために２乗法を用いることが合理的。
    →まだ表面的な理解に留まっているので繰り返し読み込む

2.中心極限定理

  • 分布パターン作成の原点
  • 様々な確率分布を合成したものはきれいな正規分布になる
  • バイアスの法則性をどう導入するか
  • 金融市場の振る舞いを攻略するためのツール
  • 正規分布と古典統計が土台となる

3.確率過程

  • ブラウン運動の考え方をベースに「絶対値ゲーム」の構造を作る
  • 時間経過とともに拡散範囲が増大する
    →拡散半径はtの平方根(t=経過時間)
  • ベクトルの絶対値という捉え方に基づいて、３次元や１次元でも同様の仮定が可能
  • 相殺メカニズムには2種類ある
    →①「+と−の2極相殺メカニズム」と②「サンプルのばらつきによる相殺メカニズム」
    →①の方が②よりも強力
  • 「絶対値ゲーム」では、①の効果がオフになっているため、時間の経過とともに儲けが増える
    →したがって「どうやって絶対値ゲームを導くか」が重要となる
  • 運動が上向きの曲線ならば、儲けを出す絶対値ゲームが作れる
    →ペアトレードと無リスクポートフォリオの作成において有効な考え方
  • 曲線的な連動性とボラティリティに注目する
  • 金融領域では、数学のテクニックを駆使して、連動曲線をいくつかのパーツに分解して、その中から放物線のパターンを抽出する(伊藤のレンマ)

【雑感①】

【バイアスとの付き合い方】

バイアスから逃れられないのであれば、それをうまく使う方法を考えた方が良い。 バイアスの多様性を理解すれば、事象から法則性をたくさん導くことができるようになる。 やはり、学問は良いものだ。新たな経験を導くきっかけにもなるし、一人でゆっくり読書する時間があるのはありがたい。

【トレンドよりボラティリティ】

トレンドを読む力よりもボラティリティを観測する力を磨く方がBotterとして有利。 トレンドは未来のことで不確定だからそれを正確に予測することができないが、ボラティリティは現実に起こっている事象だから、誰でも観測できる。 その解釈の仕方や実行する戦略において差が生まれる。

近い未来の予測もボラティリティの観測を土台にしているので、やはり現在の状況を正しく認識する力を付けることは優先順位の高い課題だ。 現状認識が間違っていると将来の予測もおかしなことになる。 これまでは誤差を修正する力を磨いてきたが、観測する力もまた重要なのでこれを磨くことに注力する。

最近はクォンツ的な発想になるようにインプットを絞り込んでいるから、こういう発想になる。 偏りを作らずバランスよく生活することも大事だが、個人的には一定期間バランスを崩すくらいの極端な学び方や訓練をするのが好きなので、引き続きBotterとしてのポジションで振る舞うようにする。

【確率微分方程式】

  • 一定方向への動きとランダムなシグザグ運動を分離する方法
  • dx=Adt+Bwt
    →Adtはトレンド、一定方向に動く部分
    →Bwtはボラティリティ、ランダムなジグザク運動
  • 伊藤のレンマを土台にしている

【伊藤のレンマ】

  • ジグザグ運動の問題を解決する手法。
  • 2つの部分を綺麗に分離できる
  • テイラー展開で近似を見
  • 経過時間に相関するランダムな運動を定義できる
  • 多段式の連動構造も分離できる
  • ボラティリティの相殺メカニズムを説明できる
  • デルタの算出をして無リスクポートフォリオを作るのに役立つ

【実際のブラック・ショールズ理論】

  • 権利＝オプションの値段を求める方程式
  • 権利行使点を境にそれ以降の期待値を求める
  • 難所①：フーリエ級数の利用
    →様々な三角関数の和であらゆる関数を表す
  • 難所②N(・)の利用
    →正規分布グラフに基づく積分から期待値を求める統計的手法

【測度とルベーグ積分】

現実の確率統計の場面で表面化することはあまりないため、大まかに知っておけば良い。現実には問題全体が比較的早い段階で連続的なアナログ量に近似されるので、このアプローチが必要になるのはより抽象度の高い問題を扱うケースになる。

  • 不連続な関数を扱う
  • 無限小部分の面積を求める
  • デジタル(不連続)→アナログ(連続)への変換
  • 集合の概念を用いる

【雑感②】

確率統計理論の土台になっている考え方をその発生から歴史的な流れに基づいて知る学ぶことができた。 基礎理解の部分を地道に積み上げて理解することなしに発展的な内容を導くことは非常に難しいのかもしれない。感覚的に理解していたことを理論立てて学び直す大切さも再確認できた。

理論ばかりを学んでいてもバランスが悪いので、自分の経験から得た具体的なモデルに当てはめて説明ができるように行動量を増やす。

アービトラージ入門を読んで学んだこととの相関を深く実感した。マインドマップを再読しながら、ブラックショールズ理論の理解をもう１段階深めて、新しい戦略構築創出の基盤を固めたい。また、ヘッジの重要性についても考えさせられた。

そのリターンに応じたリスクを取ることができるのであれば、敢えてヘッジしないことで資金効率を高めることできる。その点は期待値や試行回数との兼ね合いで決めたい。 一見ランダムに見える確率の中に法則性を見出して、金融を攻略しようというアプローチができるのはとても面白い。

また、発生がランダムな事象についても「その方向性を見出すことで継続的に利益を出し続ける手法を編み出す」という思考フローには再現性がある。 構造を見抜いて適切な手段を取ることができるように、知識の蓄積をしておいて損はない。専門外のことからも学び続ける仕組みを無くさないようにする。

【宿題】

  • オプション戦略における無裁定モデルを作成する
  • →運用結果が想定通りになっているのかを検証する
  • より単純なモデルを作れないかどうかを検討する
  • 経済数学の直感的方法（マクロ経済学編）を読む

まとめ

今まではなんとなく感覚で理解していたことが、数式に基づいて説明できることが分かったのでスッキリしました。

今回の学びは、Bot開発においてすぐに効果を発揮するエッジではありません。

しかし、基礎部分の理解という意味では、時間が経っても効果をか発揮し続けるエッジであるとも言えます。

Yodaka

今後も継続してBot開発に関係する知識と体系的理解を広げていきます。

関連記事
仮想通貨botの開発記録#51(2024/2/3)「仮想通貨Botterの必読書シリーズ②アービトラージ入門」

続きを見る

-Bot, トレードロジック, 書籍・論文・web記事